Projects done during PhD at RPI
Performance benchmark for a sparse linear system solver
Numerical simulation of systems governed by partial differential equations ultimately leads to solving massive systems of linear equations. We present a parallel conjugate gradient solver which employs a memory efficient Compressed Row Storage data-structure.
...
Two versions of the solver, a CPU only (MPI) and CPU-GPU (CUDA) are developed and compared in this study. The CPU only version of the solver exhibits speedup with increase in number of processors. The CPU-GPU solver although is faster, doesn’t show any scaling which needs further investigation. But overall, we are able to demonstrate the effectiveness of parallel conjugate gradient solver which is a key to faster simulations. Detailed final report for the project can be found here
Uncertainty quantification and mesh adaptivity for fluid-flow over uncertain geometry
Adaptive meshes are very useful in the context of solving complex engineering problems as they offer the flexibility to use coarser mesh everywhere but at locations of interest and/or at locations of complex solution behavior. More accurate prediction of the solution can be computed with better efficiency using adaptive meshing than using finer mesh throughout the problem domain. ...
Mesh adaptation process typically involves computing the solution on a coarse mesh, and based on some error parameter, the locations of complex solution behavior is identified and the mesh is refined at these locations. When uncertainties are involved in a problem, it is not wise to demand the mesh to be refined adaptively every time the solution is computed (since the solution is computed numerous times for different realizations of the uncertain parameters). In this project, a method to identify an adapted mesh (which was adapted for some previous realization) and use it for a current realization (based on the compatibility of said adapted mesh for the current realization) is proposed. By eliminating the process of repeating the redundant adaptation steps, significant computational time is saved. Detailed final report for the project can be found here
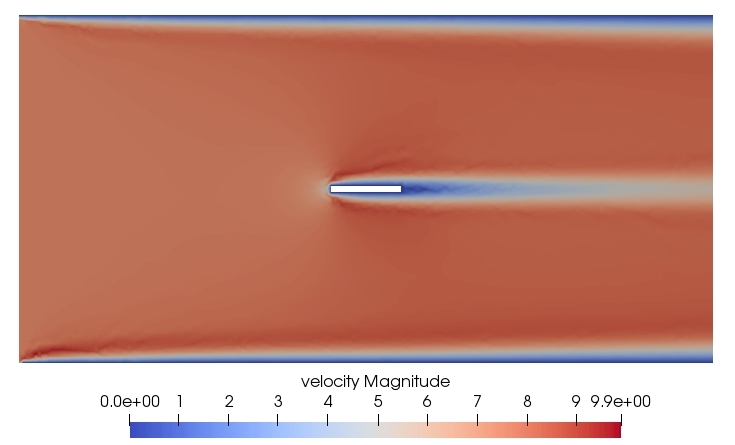
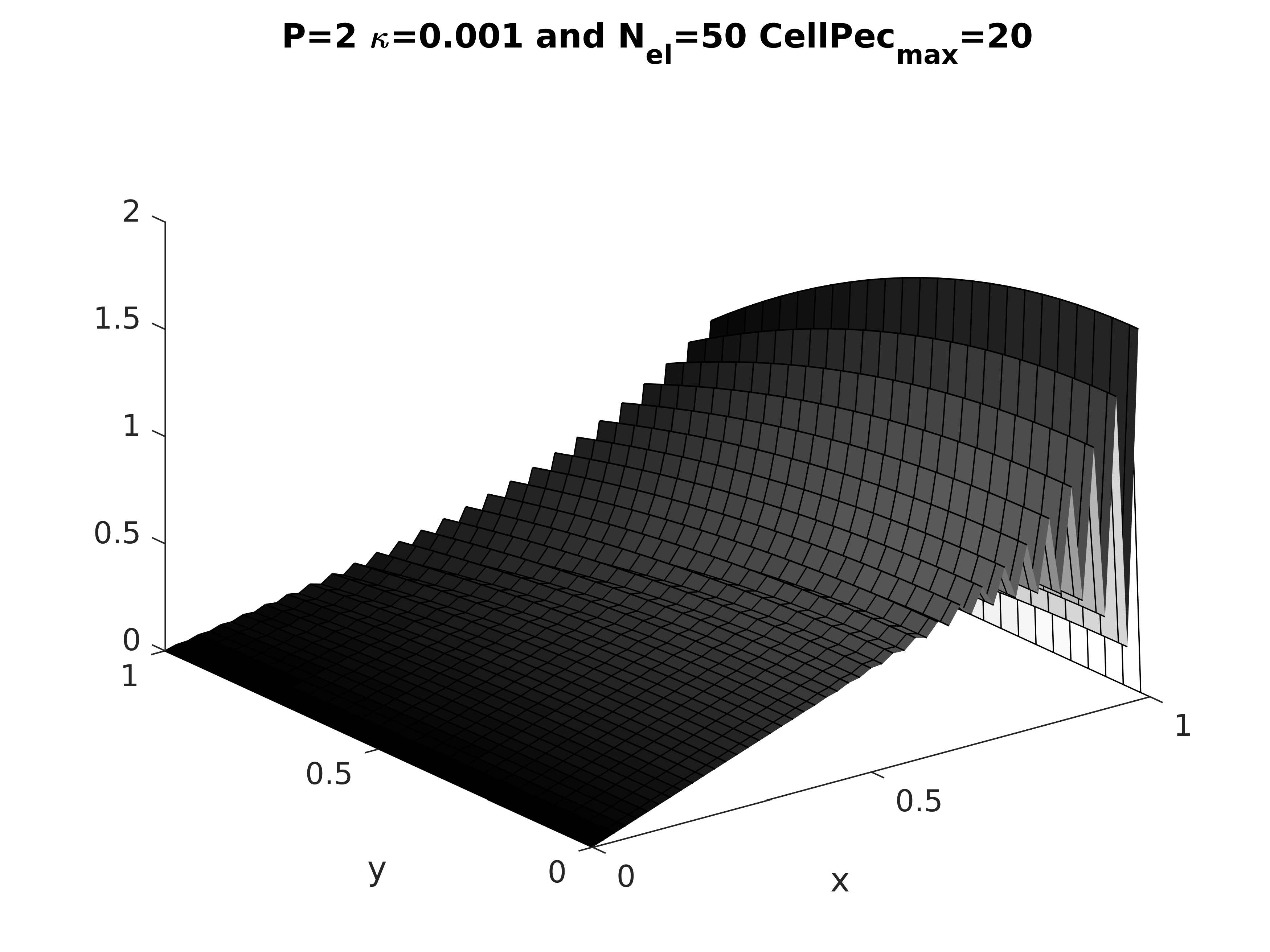
Stochastic VMS for 1D fluid-flow systems
The Variational Mulitscale formulation for deterministic and stochastic problems in 1D Advection Diffusion and 1D Burgers Equation with dirichlet boundary condition are presented in this report. Linear finite element shape functions are used to represent the physical domain, and spectral basis are used for stochastic domain.
...
The VMS formulation, in general requires a stabilization parameter to be defined which is a function of the advection and diffusion parameter in the equation. The stochasticity of the problem is assumed to be contributed by either an uncertain advection term or uncertain boundary condition. Therefore, in the these cases the stabilization parameters are itself an uncertain term. For the sake of convenience, the stabilization parameters are approximated with their projection in generalized Polynomial chaos (gPC) basis. The unstability of Galerkin methods for advection dominated problem is also highlighted in this work. Detailed final report for the project can be found here
Projects done during Master's at IITM

Design and Development of Scope-I
Scope-I (by Detect Technologies) is one of kind robot that perform visual inspection and automatic analysis for pipeline stacks (in Economizers and Superheaters) in Thermal power plants. This robot was intended to reduce the shut-down of a power plant for the inspection process by 60%.
...
I led/managed a team of ten during the course of this project. There were 3 main objectives. Firstly, to design and optimize the basic and chassis model and make it available for a wide range of powerplants with different configurations of pipeline-stacks. Secondly, to design and fabricate a robotic arm and actuator mechanism (on which the camera is mounted) to help inspection of spaces between the pipelines. Finally, the designing of electronics and control system for the robot. All the objectives were met and demonstrated during the final presentation of the project
Simulation of systems using Variational principles
Variational principles are mathematical techniques implemented to optimize (extremize/minimize) a function in calculus. It is also very much effective in formulating the motion equations of a physical system. Especially for complex systems like double pendulum this technique is much more efficient and simple. ...
In this project two such complex systems (double compound pendulum and double spherical pendulum) were taken and using variational principles the motion equations were formulated. In addition to formulation of motion equations, for a given set of initial conditions the motion was also simulated. The project was completely done on the symbolic computation software - Mathematica.

